1. Introducción.
Para conocer el mundo que nos rodea, comprender los fenómenos que en él suceden y lograr el progreso de la ciencia y la tecnología, siempre ha sido necesario medir con la exactitud y la incertidumbre requeridas, tal como preconiza la metrología, ciencia de la medida.
Los descubrimientos y los avances en el conocimiento que observamos a diario en cualquiera de los campos, no serían posibles sin instrumentos de medida, desde un microscopio de fuerza atómica hasta un radiotelescopio. Pero el desarrollo y la utilización de dichos instrumentos deben seguir unos principios metrológicos clave, a fin de obtener resultados exactos y trazables a las unidades fundamentales de medida, haciéndolos así válidos y comparables.
Según el Vocabulario Internacional de Metrología [1], magnitud es la propiedad de un fenómeno, cuerpo o sustancia, que puede expresarse cuantitativamente mediante un número y una referencia, habitualmente una unidad de medida. De esta forma, el valor Q de cualquier magnitud medida puede expresarse como el producto {Q}×[Q], siendo {Q} su valor numérico y [Q] la unidad de medida empleada.
El actual sistema SI es el adoptado internacionalmente para la práctica científica y el único legal en España [2], en la Unión Europea y en la mayoría de los países del mundo. El SI parte de un pequeño número de magnitudes básicas, con sus correspondientes unidades, definiendo, a partir de ellas otras derivadas, como producto de potencias de las básicas, elevadas a exponentes específicos.
Las magnitudes básicas del actual SI son: longitud, masa, tiempo, intensidad de corriente eléctrica, temperatura termodinámica, cantidad de sustancia e intensidad luminosa, siendo sus correspondientes unidades SI: metro, kilogramo, segundo, amperio, kelvin, mol y candela.
El SI ofrece además una serie de prefijos, de gran utilidad para expresar los valores de magnitudes mayores y menores que la unidad SI correspondiente, que permiten formar múltiplos y submúltiplos decimales de dichas unidades [3].
2. Evolución y revisión del SI
En 1960 la 11ª Conferencia General de Pesas y Medidas (CGPM), en su Resolución 12, definió y estableció formalmente el SI [4], a partir del anterior sistema métrico decimal. Desde entonces se ha revisado de cuando en cuando, en respuesta a las necesidades de la ciencia y la tecnología.
El SI es un sistema coherente de unidades que permite cuantificar cualquier magnitud medible de interés en la investigación, la industria, el comercio o la sociedad, en campos tan variados como la salud, la seguridad, la protección del medio ambiente, la adquisición de bienes o la facturación de consumos, por citar algunos ejemplos. Por ello, cualquier científico o persona involucrada en cualquiera de las ramas del conocimiento, incluyendo la enseñanza en cualquiera de sus niveles, debe estar familiarizada con él.
Los Estados adheridos a la Convención del Metro representan hoy en día alrededor del 98 % de la economía mundial, por lo que el SI es la base misma del comercio internacional y el soporte de la infraestructura metrológica mundial, a través de los institutos nacionales de metrología.
La revisión del SI surgió para dar respuesta a las cada vez mayores exigencias científico-tecnológicas, que requieren menores incertidumbres de medida (1) en todos los campos para poder garantizar con la mayor seguridad desde resultados de experimentos que confirmen hipótesis de teorías físicas, hasta el cumplimiento de las estrechísimas tolerancias de fabricación exigidas hoy en día en la industria o en campos como el de las nanotecnologías.
Ya en el pasado, Maxwell y Planck apuntaron las ventajas de un sistema de unidades de medida basado en constantes universales. Maxwell dijo(2): “Si deseamos obtener patrones de longitud, tiempo y masa que sean absolutamente permanentes, tenemos que buscarlos no en las dimensiones, el movimiento o la masa de nuestro planeta, sino en la longitud de onda, el periodo de vibración y la masa absoluta de las moléculas, imperecederas, inalterables y perfectamente iguales unas a otras”. También Planck(3) manifestó “…con la ayuda de constantes fundamentales tenemos la posibilidad de establecer unidades de longitud, tiempo, masa y temperatura, que necesariamente mantengan su importancia en todas las culturas, incluso las extraterrestres y no humanas”.
Por tanto, la ligazón a constantes universales de las unidades de medida permitiría la reproducibilidad en cualquier tiempo y lugar de sus realizaciones prácticas, abandonando definitivamente los patrones materializados, cuya propiedad fundamental debía ser la estabilidad pero que, como en el caso del kilogramo, han mostrado sus limitaciones.
Sin embargo, adjudicar el valor unidad a las constantes naturales, como propuso Planck, conduciría a valores nada prácticos de las unidades de longitud, tiempo, masa y temperatura(4), muy alejados de la dimensión “humana” que, desde el comienzo de la historia, utilizamos en nuestra vida diaria.
Así pues, aunque el SI revisado retoma en cierto modo la vía sugerida años atrás por Planck, Maxwell y otros, al basarse en constantes universales, dadas sus ventajas en cuanto a perdurabilidad, lo hace, no partiendo de valores unitarios de las constantes, sino de sus valores numéricos actuales, obtenidos experimentalmente a partir de las unidades SI utilizadas hasta ahora.
Por ello, la Resolución 1 de la CGPM en su 24ª reunión de 2011 propuso ligar las definiciones del kilogramo, amperio, kelvin y mol, a valores numéricos exactos de la constante de Planck h, la carga elemental e, la constante de Boltzmann k y la constante de Avogadro NA, respectivamente. También propuso actualizar la redacción de todas las definiciones de las unidades SI, de forma que fueran más homogéneas entre sí y aparecieran de manera explícita las constantes utilizadas en su revisión.
Sin embargo, posteriormente, la Resolución 1 de la CGPM, en su 25ª reunión de 2014 [5], consideró que, a pesar de los progresos ciertos realizados hasta entonces, los datos disponibles sobre la determinación de h, e, k y NA y sus incertidumbres, aún no eran lo suficientemente robustos como para poder adoptar la revisión del SI, por lo que hubo que esperar al 16 de noviembre de 2018, para obtener su aprobación por la 26ª CGPM.
En el SI anterior, las unidades básicas, sobre todo las basadas en patrones materializados, tenían asignada por definición una incertidumbre nula. Y las mediciones experimentales realizadas con esas unidades, entre ellas las de las constantes fundamentales, tenían una incertidumbre asociada. En el momento del paso al SI revisado cambia el esquema, atribuyéndose incertidumbre nula a los valores numéricos de las constantes elegidas. En ese mismo instante las unidades “heredan” las incertidumbres anteriormente atribuidas a los valores numéricos de las constantes. Andando el tiempo, en el SI revisado las unidades se mantendrán y evolucionarán de forma experimental, por lo que contarán con una incertidumbre asociada a su realización práctica. Es de suponer además que dicha incertidumbre vaya disminuyendo, a medida que la ciencia y la tecnología progresen.
[1] Nota del Autor: La incertidumbre de medida caracteriza la dispersión de los valores atribuidos a un mensurando, informándonos sobre el intervalo en el que, con determinada probabilidad, cabe esperar encontrar el resultado de medida, aportando pues una información cuantitativa valiosa de la calidad de la medición. El concepto de incertidumbre va más allá del concepto de error, al considerar la influencia de las propias correcciones de los errores como fuente de incertidumbre, existiendo métodos internacionalmente aceptados para su estimación. Véase la Guía para la expresión de la incertidumbre de medida, 3ª ed., 2009, publicada por el CEM. https://www.cem.es/sites/default/files/gum20digital1202010.pdf).
[2] “Yet, after all, the dimensions of our earth and its time of rotation, though, relatively to our present means of comparison, very permanent, are not so by any physical necessity. The earth might contract by cooling, or it might be enlarged by a layer of meteorites falling on it, or its rate of revolution might slowly slacken, and yet it would continue to be as much a planet as before. But a molecule, say of hydrogen, if either its mass or its time of vibration were to be altered in the least, would no longer be a molecule of hydrogen.
If, then, we wish to obtain standards of length, time and mass which shall be absolutely permanent, we must seek them not in the dimensions, or the motion, or the mass of our planet, but in the wave-length, the period of vibration, and the absolute mass of these imperishable and unalterable and perfectly similar molecules”. Discurso ante la sección de física de la Asociación Británica para el Avance de las Ciencias, Liverpool, 1870.
[3] “…with the help of fundamental constants we have the possibility of establishing units of length, time, mass and temperature, which necessarily retain their significance for all cultures, even unearthly and nonhuman ones”, Ann. Physik 1, 69-122 (1900).
[4] Para c = ħ = G = ke = k = 1, siendo c la velocidad de la luz, ħ la constante reducida de Planck (h/2π), G la constante gravitacional, ke la constante de Coulomb (1/4πε0) y k la constante de Boltzmann, se obtienen los valores 4,13 × 10-35 m, 5,56 × 10-8 kg, 1,38 × 10-43 s y 3,50 × 1032 K para las unidades de Planck de longitud, masa, tiempo y temperatura, respectivamente.
3. Naturaleza de las constantes definitorias del SI
La ventaja de utilizar una constante para definir una unidad es que desconecta la definición de la realización, ofreciendo la posibilidad de desarrollar realizaciones prácticas completamente diferentes o nuevas y mejores, a medida que las tecnologías evolucionan, sin necesidad de cambiar la definición.
Las siete constantes definitorias se han elegido de forma que proporcionen referencias fundamentales, estables y universales y que, al mismo tiempo, permitan realizaciones prácticas de las unidades, con las menores incertidumbres. Como hemos dicho en la introducción, las constantes elegidas poseen distinta naturaleza, habiendo desde constantes fundamentales hasta constantes técnicas.
Por ejemplo, tanto la constante de Planck h como la velocidad de la luz en el vacío c son fundamentales, ya que determinan los efectos cuánticos y las propiedades del espacio-tiempo, respectivamente, y afectan a todas las partículas y campos por igual, en todas las escalas y en todos los entornos.
La carga eléctrica, por su parte, es una propiedad física intrínseca de algunas partículas subatómicas que se manifiesta mediante fuerzas de atracción y repulsión entre ellas a través de campos electromagnéticos. La interacción electromagnética entre carga y campo eléctrico es una de las cuatro interacciones fundamentales de la física y tiene naturaleza discreta, según demostró experimentalmente Robert Millikan [6]. La carga elemental e es la unidad más elemental de carga, siendo la que posee el electrón. El flujo de cargas elementales por unidad de tiempo es lo que denominamos intensidad de corriente eléctrica.
La constante de Boltzmann k corresponde a un factor de conversión entre las magnitudes temperatura (con unidad kelvin) y energía (con unidad julio).
La frecuencia ΔνCs del Cesio, correspondiente a la transición hiperfina del estado fundamental no perturbado del átomo de cesio-133, tiene el carácter de parámetro atómico. La estabilidad de dicha transición la convierte en una buena elección como referencia práctica.
La constante de Avogadro NA corresponde a un factor de conversión entre la magnitud cantidad de sustancia (con unidad mol) y la magnitud conteo de entidades (con unidad uno, símbolo 1). Por tanto, tiene el carácter de constante de proporcionalidad, similar a la constante de Boltzmann k.
Finalmente, la eficacia luminosa Kcd es una constante técnica que proporciona una relación numérica exacta entre las características físicas de la potencia radiante que estimula el ojo humano (W) y la respuesta fotobiológica de éste.
4. Criterios previos a la revisión del SI
Para poder aprobar el nuevo SI revisado, los distintos Comités Consultivos del Comité Internacional de Pesas y Medidas (CIPM) establecieron unos requisitos previos con el fin de, por una parte, mantener la continuidad del propio SI y, por otra, determinar los valores numéricos de las constantes sobre las que fundamentar el nuevo SI, con las menores incertidumbres posibles.
Así, para el caso de la unidad de masa, el Comité Consultivo de Masa (CCM) estableció, entre otros requisitos, los dos siguientes [7]:
- Que al menos tres experimentos independientes, incluyendo el de la balanza de potencia de Kibble y el de la esfera de Silicio, permitieran determinar el valor de h con una incertidumbre relativa ur(h) inferior o igual a 5 × 10-8.
- Que al menos uno de dichos experimentos contara con una incertidumbre relativa ur(h) inferior o igual a 2 × 10-8.
El cumplimiento de los anteriores criterios no solo beneficiaría al kilogramo sino, también y simultáneamente, al amperio, dada la dependencia de los fenómenos cuánticos eléctricos de los valores de h y e, a través de las constantes de Josephson (2e/h) y de von Klitzing (h/e2), y al mol, dada la ligazón entre NA y h, a través de la constante de Rydberg.
Por su parte, para implantar la nueva definición del kelvin, basada en el valor numérico de la constante de Boltzmann k, el Comité Consultivo de Termometría (CCT) requirió [8]:
- una incertidumbre relativa ur(k) en la determinación de k, inferior a 1 × 10-6,
- que la determinación de k estuviera basada en al menos dos métodos diferentes, cada uno de los cuales tuviera al menos un resultado con incertidumbre típica relativa inferior a 3 × 10−6.
5. Experimentos para la obtención de los valores de las constantes
Para poder cumplir los requisitos anteriores, hace años que venían realizándose distintos experimentos.
Entre estos podemos citar, en relación con la determinación de la constante de Planck h, el de la balanza de potencia, o balanza de Kibble, denominada así en homenaje y reconocimiento de Bryan Kibble quien, en 1974, ya lanzó la idea de esta balanza. En relación con la determinación de la constante de Avogadro NA, el experimento utilizado fue el de la esfera de Silicio, conocido también como XRCD (X-ray crystal density).
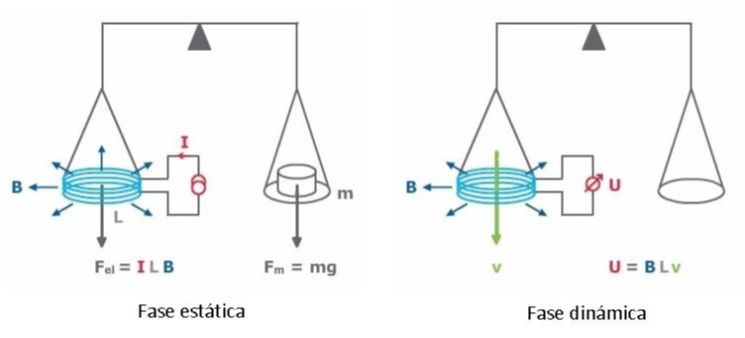
5.1 Experimento de la balanza de potencia de Kibble [9]
La balanza de potencia de Kibble permite igualar la potencia mecánica a la eléctrica, determinando el valor de h en función de la masa m utilizada en la balanza y de otras unidades obtenidas experimentalmente con muy baja incertidumbre, como son el metro y el segundo.
En la fase estática del experimento, la fuerza ejercida por la gravedad sobre la masa m; es decir, su peso, igual a mg, se contrarresta con la fuerza de Lorentz producida en una bobina de longitud L recorrida por una intensidad I, suspendida dentro de un campo magnético radial B (ILB), de donde m·g = I·L·B.
En la fase dinámica, la bobina se mueve verticalmente con velocidad constante v, dentro de un campo magnético radial B, originando una tensión U, de valor L·B·v.
Igualando entre sí el valor de L·B en ambas expresiones, se obtiene m·g·v = U·I.
En la parte izquierda de la igualdad, g se determina utilizando un gravímetro absoluto(5), y la velocidad v mediante interferometría láser.
En la parte derecha, U se determina con baja incertidumbre a partir de un patrón de tensión basado en el efecto Josephson. Por su parte, la intensidad I se determina a partir de la caída de tensión en una resistencia calibrada frente a una resistencia Hall cuántica.
De esta forma se obtiene m·g·v = U·I = K·h·fJ·fJ’, o bien, h = m× g ×v / K × fJ × fJ ‘ donde K es un coeficiente de calibración, y las fJ son frecuencias de microondas, con las que se irradia la unión Josephson.
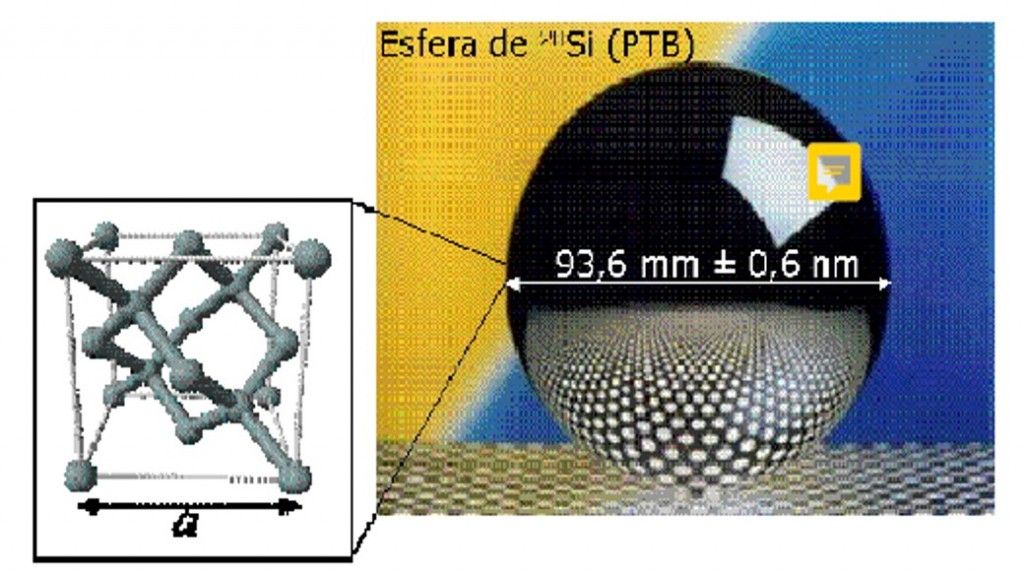
5.2 Experimento de la esfera de Silicio
La constante de Avogadro NA es la constante física fundamental que relaciona cualquier magnitud a escala atómica con su correspondiente a escala macroscópica, representando el número de partículas elementales (usualmente átomos o moléculas) contenidos en un mol de cualquier sustancia.
Para la determinación de NA se empleó el experimento XRCD (X-ray crystal density) [10], que trata de contar el número de átomos contenidos en una esfera de 1 kg, de 28Si con una pureza isotópica del 99,995 %, aprovechando la disposición ordenada del cristal.
El objetivo del experimento es en realidad doble; por un lado, obtener el valor de NA con una incertidumbre típica relativa ur(NA) inferior a 2 × 10−8 (lo que equivale a contar 100 millones de átomos y errar en 2) y por otro, determinar la masa de la esfera, de manera independiente a otras referencias de la misma magnitud, y emplearla para obtener una verificación, por esta vía, del valor de la constante de Planck h que resulta del experimento de la balanza de Kibble.
En el experimento XRCD se mide el espaciamiento a = d220 (arista de la celda unidad) de la red del silicio, del orden de 0,543 nm, mediante difracción de rayos X, obteniéndose el nº de átomos en la esfera como 8 veces el cociente entre el volumen de la esfera (determinado a partir de la medición de múltiples diámetros mediante interferometría de Fizeau) y el de la celda unidad, dado que esta, debido a la disposición de los átomos, contiene ocho átomos.
Los valores de las distintas constantes y sus incertidumbres, según el último ajuste por mínimos cuadrados realizado por CODATA en 2017, sobre los resultados procedentes de estos y otros experimentos no presentados aquí, son los siguientes: [11]
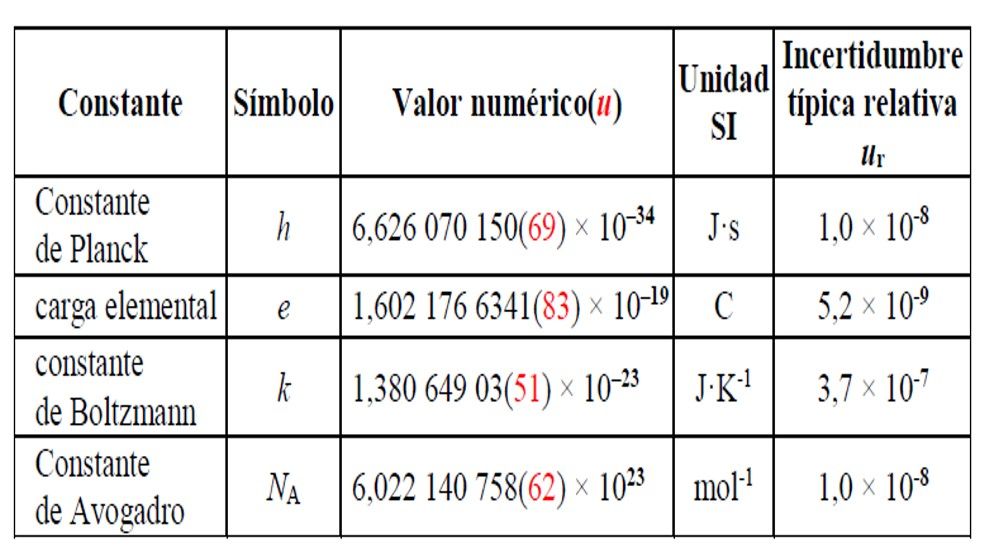
Tabla 1: Valores CODATA 2017 recomendados para h, e, k y NA.
Entre paréntesis, los valores de las incertidumbres típicas asociadas.
[5] El principio del gravímetro absoluto se basa en observar la caída-libre de un retrorreflector contenido en una cámara sin fricción. La caída libre en el vacío se repite gran número de veces, realizándose mediciones de posición y tiempo mediante interferometría láser, ya que el camino óptico hasta el retrorreflector en caída libre es el brazo de medida de un interferómetro de Mach-Zender, mientras que el brazo de referencia fijo se halla en la masa de un sismómetro activo de largo periodo, que actúa como sistema de referencia inercial.
Cuando cae el retrorreflector (masa de prueba), la sucesión dinámica de franjas de interferencia que se observa a la salida del interferómetro es detectada con un fotodiodo de avalancha, midiéndose el tiempo de paso de la interferencia constructiva mediante un reloj atómico. La longitud de onda de referencia es la de un láser de He-Ne estabilizado sobre Iodo, cuya incertidumbre es del orden de 10-11.
Para obtener el valor final de la gravedad se aplican correcciones al valor medido (por mareas terrestres, carga oceánica, efectos del clima local, efectos del movimiento polar, etc.). La incertidumbre de medida es del orden de los μGal (10-8 m/s2), según datos obtenidos en comparaciones internacionales de gravímetros auspiciadas por el Bureau International des Poids et Mesures (BIPM), como la CCM.G-K2. – Nota: el gal, símbolo Gal, es una unidad no perteneciente al SI, pero aceptada en los campos de la geodesia y la geofísica.
6. Aprobación del si revisado, por la CGPM
Tras los resultados obtenidos en los experimentos anteriores y en otros no descritos aquí, que demuestran el cumplimiento de los requisitos previamente establecidos (véase la tabla anterior), el SI revisado fue aprobado por unanimidad en la 26ª CGPM, el 16 de noviembre de 2018, acordándose su entrada en vigor el 20 de mayo de 2019, con objeto de hacerlo coincidir con el Día Mundial de la Metrología en el que, como hemos dicho antes, se conmemora la firma del Tratado de la Convención del Metro en 1875, el más antiguo que existe en vigor.
En virtud de la Resolución 1 de la 26ª CGPM [12], el SI revisado quedó definido como aquel en el que:
- la frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, ΔνCs, es 9 192 631 770 Hz,
- la velocidad de la luz en el vacío, c, es 299 792 458 m/s,
- la constante de Planck, h, es 6,626 070 15 × 10-34 J s,
- la carga elemental, e, es 1,602 176 634 × 10-19 C,
- la constante de Boltzmann, k, es 1,380 649 × 10-23 J/K
- la constante de Avogadro, NA, es 6,022 140 76 × 1023 mol-1,
- la eficacia luminosa de la radiación monocromática de 540 × 1012 Hz, Kcd, es 683 lm/W.
con los valores numéricos indicados carentes de incertidumbre y donde las unidades hercio, julio, culombio, lumen y vatio, con símbolos Hz, J, C, lm y W están relacionadas, respectivamente, con las unidades básicas segundo, metro, kilogramo, amperio, kelvin, mol y candela, con símbolos s, m, kg, A, K, mol y cd, mediante las expresiones Hz = s–1, J = kg m2 s–2, C = A s, lm = cd m2 m–2 = cd sr y W = kg m2 s–3.
6.1 Nuevas definiciones de las unidades básicas
En el SI revisado las nuevas definiciones del kilogramo (kg), amperio (A), kelvin (K) y mol (mol) están referenciadas, respectivamente, a las constantes h, e, k y NA, pero todas las definiciones de las unidades, tanto las citadas como las del metro (m), segundo (s) y candela (cd) varían su redacción, de manera que resulten más homogéneas entre sí e incluyan, de forma explícita, los valores numéricos de las constantes de las que derivan, lo que conduce a las siguientes definiciones de las unidades básicas:
El segundo
El segundo, símbolo s, es la unidad SI de tiempo. Se define al fijar el valor numérico de la frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, ΔνCs, en 9 192 631 770, cuando se expresa en la unidad Hz, igual a s-1.
De la relación exacta ΔνCs = 9 192 631 770 s-1 se obtiene la expresión para la unidad segundo, en función del valor de ΔνCs: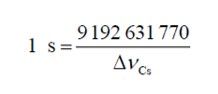
El efecto de esta definición es que “el segundo es la duración de 9 192 631 770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental no perturbado del átomo de 133Cs”.
Nota: El segundo, así definido, es la unidad de tiempo acorde con la teoría general de la relatividad. Para poder contar con una escala de tiempo coordinado, se combinan las señales de diferentes relojes primarios en diferentes ubicaciones, corregidas por los desplazamientos relativistas de la frecuencia del cesio.
El metro
El metro, símbolo m, es la unidad SI de longitud. Se define al fijar el valor numérico de la velocidad de la luz en el vacío, c, en 299 792 458, cuando se expresa en la unidad m s-1, donde el segundo se define en función de la frecuencia del Cesio ΔνCs.
De la relación exacta c = 299 792 458 m×s−1 se obtiene la expresión para el metro, en función de las constantes c y ΔνCs:
El efecto de esta definición es que “el metro es la longitud del trayecto recorrido por la luz en el vacío durante un intervalo de tiempo de 1/299 792 458 de segundo”.
El kilogramo
El kilogramo, símbolo kg, es la unidad SI de masa. Se define al fijar el valor numérico de la constante de Planck, h, en 6,626 070 15 × 10−34, cuando se expresa en la unidad J·s, igual a kg·m2·s–1, donde el metro y el segundo se definen en función de c y ΔνCs
De la relación exacta h = 6,626 070 15 ´ 10−34 kg×m2×s−1 queda definida la unidad kg×m2×s−1, de donde se obtiene la expresión para el kilogramo en función del valor de la constante de Planck h6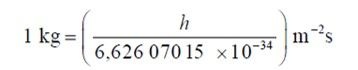
De aquí, junto con las definiciones del segundo y el metro, se obtiene la definición de la unidad de masa en función de las tres constantes h, ΔνCs y c:
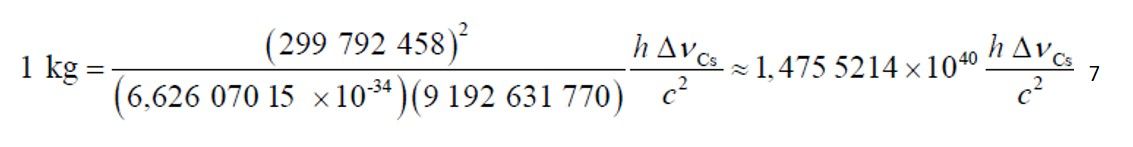
El amperio
El amperio, símbolo A, es la unidad SI de intensidad de corriente eléctrica. Se define al fijar el valor numérico de la carga elemental, e, en 1,602 176 634 × 10−19, cuando se expresa en la unidad C, igual a A·s, donde el segundo se define en función de ΔνCs
De la relación exacta e = 1,602 176 634 x 10−19 A.s se obtiene la expresión para la unidad amperio en función de las constantes e y ΔνCs: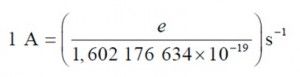
El efecto de esta definición es que “el amperio es la corriente eléctrica correspondiente al flujo de 1/(1,602 176 634 × 10−19) = 6,241 509 074 × 1018 cargas elementales por segundo”.
Nota 1: A resultas de la nueva definición, el amperio podrá obtenerse contando directamente las cargas individuales que fluyen a través de un conductor, por unidad de tiempo, empleando bombas de electrones y transistores de electrón único; es decir, circuitos eléctricos que permiten el transporte individual y controlado de electrones. Por supuesto, también podrá seguir deduciéndose a partir de las unidades de tensión y resistencia eléctricas, acudiendo a la ley de Ohm.
Nota 2: Una gran ventaja del nuevo SI es que los valores de las constantes de Josephson (KJ = 2e/h) y de von Klitzing (RK = h/e2) serán sensiblemente diferentes de los actuales, establecidos convencionalmente en 1990, pero exactos, lo que supone su vuelta al SI. Como consecuencia, será necesario aplicar una pequeña corrección del orden de 10-7 para magnitudes derivadas de la tensión, y del orden de 10-8 para magnitudes ligadas a la resistencia, allí donde la incertidumbre relativa asociada sea muy pequeña; es decir, en los institutos de metrología y en la industria puntera relacionada con patrones cuánticos basados en los efectos Josephson (KJ) y Hall cuántico (RK) [13].
El kelvin
El kelvin, símbolo K, es la unidad SI de temperatura termodinámica. Se define al fijar el valor numérico de la constante de Boltzmann, k, en 1,380 649 × 10−23, cuando se expresa en la unidad J·K-1, igual a kg·m2·s2·K-1, donde el kilogramo, el metro y el segundo se definen en función de h, c y ΔνCs
De la relación exacta k = 1,380 649 x 10−23 kg.m2.s−2.K−1 se obtiene la expresión para el kelvin en función de las constantes k, h y ΔνCs: 8
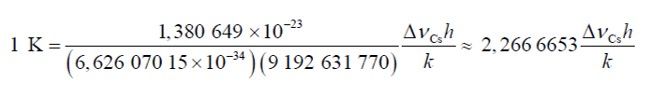
El efecto de esta definición es que “el kelvin es igual a la variación de temperatura termodinámica que da lugar a una variación de energía térmica kT de 1,380 649 × 10−23 J”.
El mol
El mol, símbolo mol, es la unidad SI de cantidad de sustancia. Un mol contiene exactamente 6,022 140 76 × 1023 entidades elementales. Esta cifra es el valor numérico fijo de la constante de Avogadro, NA, cuando se expresa en la unidad mol-1, y se denomina número de Avogadro.
La cantidad de sustancia, símbolo n, de un sistema, es una medida del número de entidades elementales especificadas. Una entidad elemental puede ser un átomo, una molécula, un ion, un electrón, o cualquier otra partícula o grupo especificado de partículas.
De la relación exacta NA = 6,022 140 76 × 1023 mol−1 se obtiene el mol en función de la constante NA:9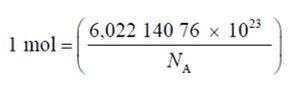
El efecto de esta definición es que “el mol es la cantidad de sustancia de un sistema que contiene 6,022 140 76 × 1023 entidades elementales especificadas”.
La candela
La candela, símbolo cd, es la unidad SI de intensidad luminosa en una dirección dada. Se define al fijar el valor numérico de la eficacia luminosa de la radiación monocromática de frecuencia 540 × 1012 Hz, Kcd, en 683, cuando se expresa en la unidad lm·W−1, igual a cd·sr·W−1, o a cd·sr·kg−1·m−2·s3, donde el kilogramo, el metro y el segundo se definen en función de h, c y ΔνCs
De la relación exacta Kcd = 683 cd.sr.kg−1×m−2×s3 se obtiene la expresión para la candela:
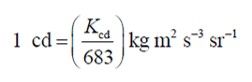 o bien, expresando kg, m y s en función de las constantes h y ΔνCs:
o bien, expresando kg, m y s en función de las constantes h y ΔνCs:
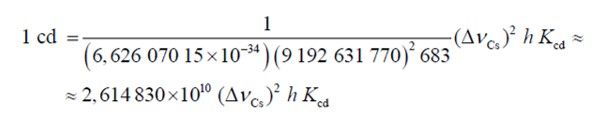
El efecto de esta definición es que “la candela es la intensidad luminosa, en una dirección dada, de una fuente que emite radiación monocromática de frecuencia 540 × 1012 Hz y tiene una intensidad radiante en esa dirección de (1/683) W/sr”.
[6] La anterior definición del kilogramo fijaba el valor de la masa del prototipo internacional del kilogramo, m(K), como exactamente igual a un kilogramo, y el valor de la constante de Planck h se determinaba experimentalmente, teniendo una incertidumbre asociada. La definición actual fija el valor numérico exacto de h y es la masa del prototipo la que hereda su incertidumbre (1 x 10−8), debiendo determinarse a partir de ahora experimentalmente. Esto mismo ocurre para el resto de las unidades.
[7] NotadelAutor: Considerando E = m.c2 = h.ν, el efecto de la definición podría ser que el kilogramo fuera la masa equivalente a la energía de 1 641 738 97 × 1023 fotones de frecuencia ΔνCs, pero es dudoso que para masas macroscópicas lo anterior sea estrictamente aplicable ya que en la práctica no es posible convertir la masa de un kilogramo en esa energía y aunque la teoría permite establecer esa relación, la definición no tendría la aplicación práctica que tiene la del metro cuando se dice que es “la distancia recorrida por la luz en una cierta fracción de segundo”.
[8] La definición anterior del kelvin establecía la temperatura del punto triple del agua, TTPW, como exactamente igual a 273,16 K. La definición actual fija el valor numérico de k, por lo que TTPW se determina a partir de ahora experimentalmente, “heredando” en el momento del cambio la incertidumbre típica relativa de 3,7 × 10−7 que poseía antes k.
Nuevos termómetros termodinámicos primarios basados en leyes físicas, permitirán medir la temperatura con muy baja incertidumbre, a partir de la medición de la energía térmica.
9 La definición anterior del mol fijaba el valor de la masa molar del carbono 12, M(12C), como exactamente igual a 0,012 kg/mol. De acuerdo con la nueva definición, M(12C) ya no es un valor exacto y debe determinarse experimentalmente. En el momento de adoptar la definición actual del mol, M(12C) pasa a tener una incertidumbre típica relativa de 4,5 × 10−10, justo la que tenía NA en el momento del cambio.
7. Conclusiones
La revisión del SI, base del comercio internacional y soporte de la infraestructura metrológica global, fue aprobada por la 26ª CGPM el 16 de noviembre de 2018, en respuesta a las nuevas exigencias científico-tecnológicas de nuestro tiempo. Dicha revisión entró en vigor el 20 de mayo de 2019, coincidiendo con el Día Mundial de la Metrología, en el que se conmemora la firma del Tratado de la Convención del Metro en 1875.
El nuevo SI define las unidades respecto a valores numéricos exactos de constantes universales bien determinadas. Entre los numerosos beneficios que esta revisión representa para la ciencia, la tecnología, la industria y el comercio, destaca la ligazón del kilogramo a un invariante de la naturaleza, como es la constante de Planck h, en lugar de a la masa de un patrón materializado, garantizando así definitivamente tanto el conocimiento de su valor “absoluto”, como su estabilidad a largo plazo.
Tras este cambio, todas las unidades cuentan ya con realizaciones prácticas reproducibles en cualquier tiempo y lugar, superando definitivamente la fase de los patrones materializados.
Respecto a las unidades eléctricas, los valores exactos de h y e suponen la vuelta al SI, con valores exactos, de las constantes de Josephson KJ = 2e/h y von Klitzing RK = h/e2, a través de los efectos Josephson y Hall cuántico. Ello supone que el amperio, el voltio, el ohmio y otras unidades eléctricas podrán obtenerse con una exactitud sin precedentes, acabando así con el sistema anterior de unidades eléctricas convencionales, situado fuera del SI.
La nueva definición del kelvin podrá realizarse mediante distintos experimentos, y en un amplio intervalo de temperaturas, frente a una propiedad del agua, su punto triple, que solo puede realizarse a una única temperatura y depende del contenido de impurezas, la composición isotópica, etc.
La redefinición del mol respecto a un valor numérico exacto de la constante de Avogadro NA, lo libera de su dependencia del kilogramo y muestra más claramente la distinción entre “cantidad de sustancia” y “masa”, algo que los químicos agradecerán.
El SI revisado no implica cambio alguno en nuestra vida diaria, garantizándose la continuidad de lo existente hasta ahora. Únicamente los institutos nacionales de metrología, que realizan mediciones de gran exactitud y baja incertidumbre, deben ajustar algunas de sus realizaciones prácticas y su diseminación, principalmente en los casos de la masa y las unidades eléctricas [13].
Finalmente, es clave que los libros de texto recojan cuanto antes este cambio, adaptado a los distintos niveles de la enseñanza, para la buena formación de los futuros profesionales, además de informar a la sociedad de la universalidad del SI e incidir en su correcta utilización, conforme a sus propias reglas de uso.
Referencias.
- JCGM 200:2012, Vocabulario Internacional de Metrología – Conceptos fundamentales y generales, y términos asociados (VIM), 3ª Edición en español 2012, Traducción de la 3ª edición del VIM 2008, con inclusión de pequeñas correcciones, http://www.cem.es/sites/default/files/vim-cem-2012web.pdf.
- Real Decreto 2032/2009, de 30 de diciembre, por el que se establecen las Unidades legales de medida. Texto consolidado. BOE nº 43, de 18/02/2010, http://www.cem.es/sites/default/files/00006981recurso.pdf
- Sistema Internacional de Unidades SI, 8ª edición 2006 (español), http://www.cem.es/sites/default/files/siu8edes.pdf
- Resolución 12 de la 11ª CGPM (1960), http://www.bipm.org/en/CGPM/db/11/12/
- Resolución 1 de la 25ª CGPM (2014), http://www.bipm.org/en/CGPM/db/25/1/
- https://es.wikipedia.org/wiki/Carga_eléctrica#Carga_eléctrica_elemental
- 14th meeting of the Consultative Committee for Mass and Related Quantities, Recommendation G1 (2013) on a new definition of the kilogram, http://www.bipm.org/en/measurement-units/rev-si/committees-si.html
- 27th meeting of the Consultative Committee for Thermometry, Recommendation T1 (2014) on a new definition of the kelvin, http://www.bipm.org/cc/CCT/Allowed/Summary_reports/RECOMMENDATION_web version.pdf
- http://www.bipm.org/en/bipm/mass/watt-balance/
- http://www.bipm.org/en/bipm/mass/avogadro/
- The CODATA 2017 values of h, e, k and NA for the revision of the SI, D B Newell et al 2018 Metrologia 55 L13
- Resolución 1 de la 26ª CGPM (2018): On the revision of the International System of Units (SI)
- CCEM Guidelines for Implementation of the ‘Revised SI’, Version 1.0, 8/12/2017.