Antecedentes
La existencia de utilidades prácticas aplicables a este tipo de conversión como la escritura dinámica de partituras musicales y la síntesis con instrumentos VST [1] evidencian la necesidad de diseño de una aplicación que ofrezca resultados fiables y robustos.
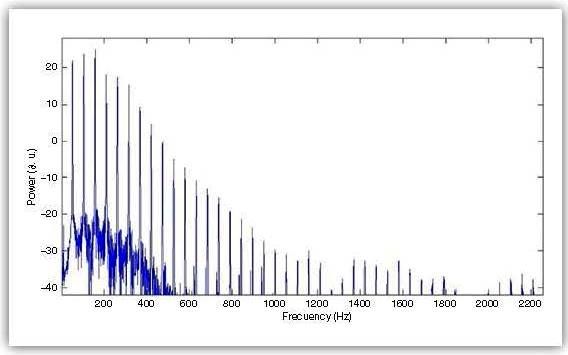
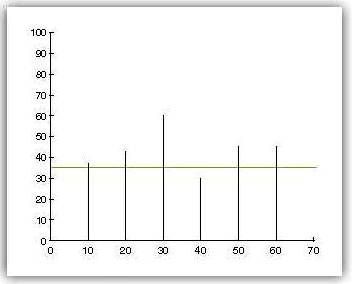
De entre las existentes aplicaciones destacan TS- AudioToMidi Converter [2] y WIDI Professional 4.0 [3]. El funcionamiento de estas se centra en la obtención del espectro armónico de la señal por medio de la Transformada Rápida de Fourier (FFT). Una vez obtenido dicho espectro armónico toman como medida de la frecuencia fundamental (Fo) que dará nombre a la nota MIDI [4] que comunicarán a la salida el pico absoluto del espectro. Este resultado que ofrecen no necesariamente será correcto debido a la propia definición de timbre de los instrumentos, pues dependiendo de qué instrumento se trate, su espectro armónico variará y con él la disposición de sus picos. Por tanto, hay situaciones en las que el pico máximo absoluto del espectro armónico de una señal no necesariamente coincide con su frecuencia funda- mental. Como ejemplo de ello, en la Figura 1 podemos observar el espectro de una nota de Trombón.
Para paliar este posible error al considerar el máximo absoluto, las aplicaciones mencionadas ofrecen la posibilidad de una ecualización para atenuar las frecuencias indeseadas, con la intención de que el usuario acote el rango de frecuencias empleado. Esta solución adoptada, aunque a simple vista pueda parecer que aporta versatilidad al poder realizar una ecualización distinta para cada caso, lo que realmente aporta es una limitación en el rango de uso de la banda de frecuencia, pues la ecualización debe empezar a atenuar desde los primeros armónicos de la nota más grave que va a interpretarse, cosa que reduce considerablemente el rango frecuencial útil del programa.
Esta limitación puede que para instrumentos de registro agudo no parezca excesivamente severa desde el punto de vista de la frecuencia, pues cuanto mayor sea la nota grave límite impuesta por el instrumento, mayor será la medida de Fo y, como consecuencia, mayor será el ancho de banda hábil. El rango de notas musicales que se podrían procesar correctamente se mantiene independientemente de su frecuencia, pero se amplía el ancho de banda cuanto más agudas sean. La consecuencia directa es que la separación de las notas en Hercios es mayor, lo que facilita la distinción de una u otra nota al estar más espaciadas en el abanico frecuencial. Esto se traduce de forma inversa en una clara dificultad añadida para los instrumentos de registro grave, donde la separación entre las notas en el ámbito de la frecuencia se reduce considerablemente. Dicha reducción implica directamente un funcionamiento deficiente de estos programas para los instrumentos con registro más grave.
Las limitaciones que acarrean los productos existentes en el mercado actual en instrumentos de viento como el Trombón han hecho evidente la necesidad de modificar los algoritmos existentes para permitir realizar con- versiones Audio-MIDI con una mayor fiabilidad y un rango frecuencial más amplio además de instrumentos cuya frecuencia fundamental no sea la del armónico con más energía.
Por tanto, se va a elegir como instrumento para los experimentos el trombón de varas. Por una parte, su registro grave ayudará a crear un algoritmo que solucione el problema de los instrumentos próximos a este registro y a su vez pueda funcionar perfectamente para instrumentos de registro más agudo. Por otra parte, como se aprecia en la Figura 1, los picos máximos del mismo, por norma general, no coinciden con la frecuencia fundamental del sonido analizado [5].
Objetivos
El objetivo principal de este trabajo es el de diseñar e implementar un plugin de audio que consiga realizar la conversión Audio-MIDI en tiempo real que se pueda emplear en un amplio rango de frecuencias y tipos de instrumentos. Esta conversión ha de asegurar unos resulta- dos fiables y acordes a la nota fundamental de la señal de entrada, además de minimizar la latencia de proceso para permitir su uso en aplicaciones de tiempo real.
La señal de entrada para el diseño de la aplicación será monofónica e interpretada por un trombón de varas. Los resultados de la conversión para dicha entrada han de ser válidos para todo su rango de frecuencias que va entre los 73 y los 587 Hercios, mientras que su rango frecuencial de armónicos sería de 1-4KHz, por lo que se tomarán en los experimentos como frecuencias de corte inferior y superior 40Hz y 4.2KHz correspondientemente.
La aplicación deberá tener en cuenta el error humano asociado al instante de la emisión de los sonidos -picado en música- y proponer una solución para las sobreoscilaciones y el ruido que aparecen en los transitorios de cada nota típicos de este tipo de instrumentos, que es justamente lo que los hace fallar con los conversores Audio-MIDI probados. Se ha elegido emplear el formato de plugin VST [1] para facilitar su posterior inclusión en cualquier programa Host que se encargue de la entrada de audio y síntesis posterior.
Estudio previo
De manera previa a la programación en tiempo real del plugin se ha realizado un estudio offline sin tener en cuenta la restricción de latencia impuesta, donde se comparan diversos algoritmos de obtención de la frecuencia fundamental, todos ellos basados en la Transformada Rápida de Fourier (FFT) y el uso de la autocorrelación.
Para las pruebas se emplearon grabaciones de audio interpretadas por el trombón de varas que abarcaran todo su rango frecuencial útil. A una misma grabación se le aplicaron todos los algoritmos de detección de pitch programados y se compararon los resultados.
Los métodos empleados en este estudio previo y que se compararán a continuación son el algoritmo de auto correlación y el algoritmo FFT simple con dos variantes en el criterio de elección de la fundamental: la elección de la frecuencia fundamental como el pico del espectro de la señal correspondiente a la menor frecuencia, y la media de las distancias entre picos consecutivos de dicho espectro, la denominada distancia espectral.
Al trabajar con frecuencias bajas del Trombón, cabe la posibilidad de que al acercarse al límite más grave de su rango, el pico relativo de menor frecuencia del espectro pueda confundirse con el propio ruido de la señal y enturbiar los resultados, induciendo inevitablemente a la elección de una Fo errónea. Por este motivo se descarta el algoritmo de elección de Fo como el pico relativo de menor frecuencia en favor del algoritmo de elección de Fo como la media de las distancias entre picos relativos del resultado de la FFT, pues aunque tratemos de convertir notas graves donde el pico correspondiente a la Fo se confunda, la disposición de los armónicos en el espectro de la señal nos dará el resultado correcto.
Con el fin de determinar el algoritmo más adecuado para la presente aplicación se ha tomado como señal de entrada la grabación de una escala musical a más de dos octavas que abarca todo el rango hábil del trombón. Se ha desarrollado un programa que ejecuta el algoritmo de autocorrelación para la obtención del pitch de las notas de la escala, que además procesa la misma señal de entrada con otro programa que basa su funcionamiento en la FFT simple, con el fin de obtener unos resultados y comparaciones de forma eficiente.
Algoritmo de Autocorrelación
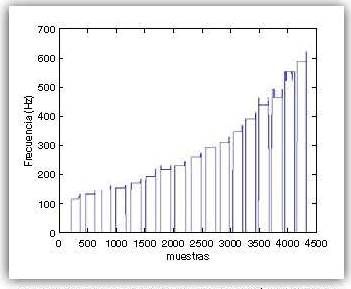
El programa desarrollado sobre Matlab® emplea la autocorrelación como herramienta para la obtención del pitch de la señal de entrada. Tras las pertinentes pruebas para el ajuste de los parámetros se han establecido una serie de valores recomendados para la obtención de la gráfica que servirá de comparativa. Se tomará una ventana de análisis de 30ms con un desplazamiento del 50%. La frecuencia de muestreo se fijará en 44100Hz. El número de puntos para realizar la FFT se establece en 4096. Con el fin de filtrar el ruido se aplicará un umbral de sonoridad de valor 0.3. Finalmente se fijan las frecuencias de corte inferior y superior en 40 y 4.200Hz respectivamente. [7]
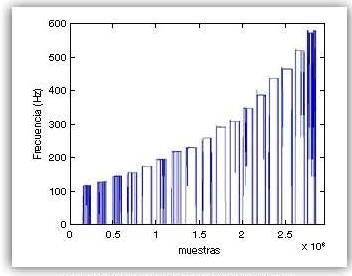
La gráfica obtenida con los valores recomendados propuestos es la de la figura 2, apreciando que en general se obtiene el valor correcto de la frecuencia, pero con muchos fallos puntuales.
Algoritmo FFT simple con medida Fo = distancia entre picos consecutivos
Análogamente al algoritmo de autocorrelación se emplea otro programa que emplea la FFT y obtiene el pitch de la información que proporciona la distribución de los armónicos en el espectro generado. Del mismo modo se han elegido unos valores recomendados para los parámetros del programa, acordes al anterior análisis para que los resultados sean ilustrativos y comparables. La ventana de análisis será de 30ms con desplazamiento del 50%. La frecuencia de muestreo de nuevo tendrá un valor de 44100Hz. Se usará un tipo de ventana Hamming para el procesado. Para la selección de máximos relativos considerados como picos del espectro de la señal correspondientes
a los armónicos de la misma se define un umbral. Se considerarán picos del espectro todo máximo relativo que supere dicho umbral. Este parámetro equivale al producto del máximo absoluto de la correspondiente FFT y un valor n<1 que decidirá cuán cerca del máximo se halla el umbral. El valor recomendado para el umbral es de 1/3 del máximo absoluto del espectro obtenido en cada caso. Se filtrará el ruido del mismo modo que en el anterior algoritmo, por medio de un umbral de sonoridad fijado a un valor de 0.3. Por último se acotan del mismo modo las frecuencias de corte otorgando un rango frecuencial de [40,4200]Hz.[6].
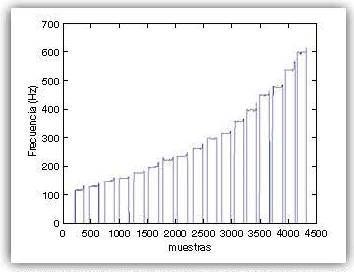
Con los valores señalados se obtiene la gráfica de la Figura 3, bastante más estable que los obtenidos con la autocorrelación (Figura 2).
Comparación de los resultados
A la vista de las gráficas obtenidas, cabe comentar lo siguiente. Por una parte habrían de analizarse las bandas pasantes de cada nota. En el caso de la autocorrelación las oscilaciones alrededor de la frecuencia correspondiente a la nota musical interpretada a la entrada son muy pequeñas, pero existen saltos a frecuencias alejadas de la deseada difíciles de corregir, especialmente en los tramos extremos (para las notas más graves y agudas del rango hábil del instrumento). En el caso de la FFT simple las oscilaciones alrededor del punto correspondiente a la frecuencia asociada a la nota de entrada son más evidentes, pero en este caso no aparecen saltos a frecuencias alejadas. Estas oscilaciones alrededor de la frecuencia de la nota se deben a la fluctuación del aire al ser emitido el sonido por parte del intérprete y son algo normal que aparecerá inevitablemente en este tipo de instrumentos. Su corrección es muy sencilla, simplemente redondeando a la nota musical más cercana. En este aspecto el funcionamiento de la FFT simple es mejor que el del algoritmo de autocorrelación.
Por otra parte se debe estudiar los flancos de subida y bajada de cada nota y las posibles sobreoscilaciones. En el caso de la FFT simple hay muchas de las notas que tienen sobreoscilaciones ya sea al inicio o al final de la banda de la nota, mientras que en el algoritmo de autocorrelación aparecen en menor medida. Estos picos hallados en los límites de las bandas de las notas se deben, una vez más, tanto al error humano como a la propia naturaleza de instrumentos de viento-metal como el trombón de varas, ya que en el instante de la emisión de la nota, así como en el instante del corte de la misma, pueden aparecer perturbaciones debidas a una incorrecta posición de la lengua al golpear el paladar.
Se puede extrapolar de este análisis que el algoritmo de autocorrelación suaviza en mayor medida las perturbaciones ocasionadas por el error humano, pero funciona bastante peor que el algoritmo FFT simple en las bandas pasantes de las notas debido a la aparición de saltos puntuales a frecuencias alejadas de la deseada. Por ello el algoritmo que se desarrollará para el plugin será el FFT simple.
Criterio de elección de la frecuencia fundamental
Para obtener la medida de la frecuencia fundamental a partir de la distancia entre armónicos consecutivos será necesario almacenar en un vector todos los máximos relativos del espectro de la señal. Como condición de máximo relativo se establece que ha de ser mayor que un umbral de amplitud. Este umbral se definirá en función del máximo absoluto. El valor del umbral se va a introducir como parámetro en la interfaz gráfica, para que pueda adaptarse según las exigencias de la señal de entrada.
Una vez guardados en memoria todos los picos relativos, se ordenarán de menor a mayor en función de su posición, no de su amplitud. Es decir, el índice del máximo relativo correspondiente a la menor frecuencia se hallará en la posición 0 del vector, mientras que el índice del máximo relativo del armónico de mayor frecuencia se situará en la última posición.
La frecuencia fundamental coincide con la distancia entre armónicos consecutivos, su distancia espectral. Este será el criterio que servirá de base para el algoritmo. Se hará uso del vector de índices comentado. No obstante, no todos los índices serán válidos. Habrá algunos casos en los que entre índices consecutivos exista otro armónico, cuyo pico no supere el umbral y no se haya almacenado. En estos casos, la distancia entre picos será el doble.
Se estudiarán en detalle las distancias espectrales entorno al pico máximo absoluto. Se asume que una única medida de distancia entre picos no es suficiente para afirmar con seguridad que se trata de Fo. Con estas premisas, el primer paso será estimar una medida inicial de Fo. Esta medida inicial será la que se use para comprobar si se repite a lo largo del espectro o si no lo hace.
Para la primera estimación de Fo se mide la distancia entre el índice del pico máximo absoluto y su armónico consecutivo, tanto por arriba como por abajo. Estas dos medidas se comparan. Si son coincidentes, aplicando un rango de tolerancia (tolerancia óptima hallada alrededor del 1%), se toma como medida inicial de Fo la media aritmética entre estas dos distancias. En el caso que no coincidan, se toma como estimación de Fo la de menor valor, pues si alguna de las dos medidas se ha saltado un armónico será la de mayor módulo.
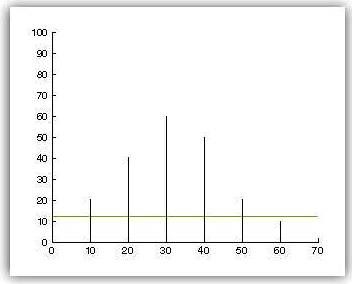
Para ilustrar esta primera estimación de frecuencia fundamental se ha simulado un espectro aleatorio. En él se aprecia que el pico máximo absoluto se halla en el armónico 3 y que el umbral de amplitud está situado al 20% de dicho pico. Puesto que los armónicos 2 y 4 superan el umbral y las distancias entre armónicos 2-3 y 3-4 son equivalentes y de módulo 10, la primera estimación de Fo será igual a 10. Se simulará otro espectro aleatorio a continuación donde uno de los armónicos consecutivos al pico máximo absoluto no supere el umbral.
En este segundo caso, la medida entre el pico máximo y el pico consecutivo inferior será de módulo 10, mientras que la distancia entre dicho máximo absoluto y su consecutivo por la derecha que supere el umbral será de módulo 20 (el armónico 4 no se almacenaría por no superar el umbral). El criterio de estimación de Fo tomaría la menor de las distancias, es decir, la de módulo 10. La estimación sería correcta.
Existen más casos posibles. Si no superara el umbral ningún armónico por la derecha del pico absoluto, pero sí por la izquierda, la estimación sería la distancia entre el pico y su armónico anterior y viceversa.
El restante caso, en el que no hay ningún armónico que supere el umbral, inhabilitaría el uso de este algoritmo, por lo que se habría de tomar como Fo definitiva el pico absoluto, aunque lo recomendable sería decrementar el valor del umbral.
Una vez se tiene la estimación de Fo almacenada en memoria, el algoritmo procederá a comprobar cuántas veces se repite esta medida a lo largo del vector donde se han ordenado los índices de los picos relativos, es decir, donde se ha almacenado el valor de los armónicos. El número de repeticiones de dicha medida se almacenará en una variable que servirá como coeficiente de seguridad. Si este coeficiente es mayor que 1, es decir, si al menos se ha repetido una vez la medida de Fo estimada, el valor de Fo estimado será válido. Para una mayor precisión, se hará la media aritmética de Fo y sus repeticiones, aunque para una tolerancia del 1% la variación será mínima, pero siempre más precisa. En el caso de no haberse cumplido la condición de que el coeficiente de seguridad sea mayor que 1, no se puede tomar este algoritmo como válido y se establecerá como Fo el pico relativo asociado a la menor frecuencia. Cuando sola- mente haya un pico que supere el umbral, este coincidirá con el pico absoluto.
Analizando de nuevo los espectros aleatorios anteriores, en el primer caso la estimación de Fo sería de valor igual a 10, y esta distancia se repetiría 4 veces a lo largo del vector, por lo que Fo definitiva sería también de valor 10 y se podría asegurar que es una medida correcta. En el segundo caso, la Fo estimada sería 10 también y esta distancia se repetiría una vez más a lo largo del vector, con lo que el coeficiente de seguridad valdría 2 y la Fo definitiva sería correcta y de valor 10.
En definitiva, el algoritmo empleado para la elección de la Fo tendrá un buen funcionamiento si previamente a su uso se ha hecho un correcto calibrado del umbral de amplitud para que se contemplen suficientes máximos relativos en los cálculos.
Filtrado de la señal
Con la finalidad de eliminar las perturbaciones halladas en la señal tras la ejecución del algoritmo FFT simple, ilustradas en la Figura 3, se han diseñado una serie de filtros. Nuevamente se realiza el diseño de los mismos de un modo offline sin tener en cuenta la restricción de latencia impuesta.
Para aplanar las bandas de las notas y eliminar las oscilaciones indeseadas se realiza un primer filtrado cuyo funcionamiento reside en la interpretación de las frecuencias con relación a las notas musicales. Cuando la frecuencia que se esté analizando no coincida con la asociada a una nota musical el filtro actuará de tal modo que dicha frecuencia tome el valor de la frecuencia asociada a la nota musical más próxima. El resultado es el de la Figura 6.
Se consigue así normalizar las zonas estacionarias de cada nota. Sin embargo, todavía faltaría por eliminar los transitorios que aparecen generalmente al principio y/o final de cada nota. Para ello se introduce un último filtro. En este caso, el algoritmo recorrerá el vector de datos de inicio a fin, parándose para cada situación de cambio de frecuencia y se comprobarán los instantes siguientes a dicha situación. Si la nueva frecuencia
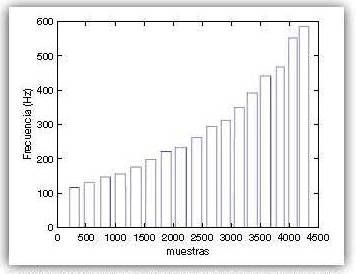
Figura 7. Resultado punto óptimo con filtro de sonoridad, de mediana, corrección frecuencial en función de las notas y filtro corrector
de saltos puntuales.
se mantiene un número de muestreos igual al parámetro introducido como condición de cambio de nota, se mantendrá el cambio de frecuencia. Si, por contra, el cambio frecuencial es de duración menor a dicho parámetro, la nueva frecuencia se descartará y se mantendrá el valor que había antes de dicho cambio. Con ello se eliminarán los saltos frecuenciales de menor duración que el parámetro introducido como condición de cambio de nota. Tomándose como condición de cambio de nota que se mantenga la nueva frecuencia 10 muestreos consecutivos -valor adaptado a la señal de entrada que se está procesando en los análisis aquí expuestos- se consiguen eliminar todas las perturbaciones y se obtiene así la señal deseada a la salida del algoritmo.
Con esto se ha conseguido obtener un resultado perfectamente afín a la señal de entrada y se han diseñado los filtros necesarios para dicho fin, con lo que es el momento de pasar al análisis en tiempo real.
Procesado y funcionamiento del Plugin
Como todo plugin de audio, MConverter tiene un módulo editor y un módulo procesador. El editor sirve como interfaz gráfica y es el encargado de comunicar al procesador el valor de los parámetros introducidos por el usuario. El procesador es el encargado de recibir los paquetes de datos, almacenarlos en un buffer, realizar las pertinentes transformaciones y filtrados a los mismos y enviar los resultados a la salida. Esta serie de operaciones se realiza cada vez que el programa Host envía un paquete de datos al plugin, cosa que sucede de forma regular y continua en el funcionamiento normal de la aplicación. A continuación se describen los pasos que realiza el procesador para cada llegada de paquete de datos:
- Lectura del paquete de datos de entrada y almacenamiento de los mismos en un buffer circular.
- Llamada a la función encargada de la obtención de la FFT y elección de la frecuencia fundamental correspondiente.
- Post procesado. Aplicación de filtros correctores y otras modificaciones aplicables a los resultados del anterior punto.
- Comunicación de los resultados por el canal MIDI.
- Actualización de las variables.
Dentro del post procesado que se menciona en el punto 3 se incluirían los filtros diseñados del siguiente modo:
- Codificación MIDI. Conversión de la información frecuencial en hercios a la codificación de notas De este modo se corrigen las desafinaciones y se eliminan las oscilaciones alrededor de notas. Esta transformación atiende a la siguiente expresión:
noteMIDI = round(69.0f + 12.0f * log2f(Fo / 440))
- Filtrado pasa-banda. Tomándose como frecuencias de corte las introducidas por el usuario en el editor, se eliminan y sustituyen por silencios (frecuencia 0Hz) las frecuencias superiores o inferiores a los límites establecidos por los parámetros correspondientes.
- Filtrado de sonoridad. Se considera silencio en los casos que no se alcance el nivel de sonoridad (intensidad de la señal) establecido por el parámetro pertinente de la interfaz.
- Transposición. Se le suma o resta el intervalo en semitonos introducido por el usuario en la interfaz, en caso de haberlo.
- Retraso corrector. Desde la interfaz el usuario puede indicar si quiere aplicar un retraso corrector al procesado o no y de cuántos instantes quiere aplicarlo. Si se introduce retraso corrector, el plugin esperaría tantos instantes (entendiendo como instante cada vez que llega un paquete de datos y se ejecuta el procesado) como se le haya indicado en la interfaz para comunicar los resultados. Si se han producido cambios de nota de duración menor a la del retraso corrector, estos serán considerados perturbaciones y eliminados en consecuencia, manteniéndose la última nota (o silencio) activa durante los instantes de perturbación.
Estos filtros obtienen sus parámetros de la interfaz, lo que dota al plugin de una gran versatilidad otorga al usuario las herramientas necesarias para adaptar cada filtro a sus exigencias.
Interfaz gráfica de usuario
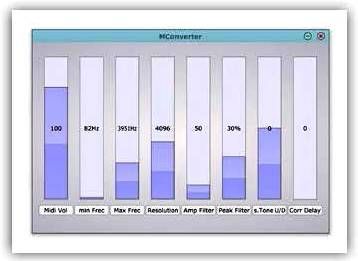
Para otorgar versatilidad al programa y posibilitar la adaptación del mismo a las necesidades del usuario se ha creado una interfaz gráfica desde la que se posibilita la modificación de los parámetros siguientes:
- Midi Vol: Control del volumen de la salida Rango [0,127].
- min Frec: Frecuencia de corte mínima. Rango [0,6.000]
- Max Frec: Frecuencia de corte máxima. Rango [1.000,12.544]
- Resolution: Resolución de la FFT. Rango [100,10.000]
- Amp Filter: Umbral del filtro de sonoridad. Rango [0,500].
- Peak Filter: Umbral para el criterio de selección de picos relativos, medido en % respecto al pico máximo. Rango [0,100] %.
- Tone U/D: Intervalo a transportar la salida MIDI en semitonos. Rango [-24,+24].
- Corr Delay: Retraso corrector de saltos. Rango [0,60].
En la figura se puede visualizar la interfaz gráfica de usuario del plugin en su estado por defecto.
Conclusiones
Si se realiza una correcta inicialización del programa, de modo que se hagan las pruebas pertinentes con el instrumento para adaptar los parámetros de la interfaz al ámbito de uso del mismo, el plugin funciona perfectamente.
Por otra parte, la condición de en tiempo real impuesta se ha logrado con una eficacia notable, puesto que la latencia que se ha medido en los experimentos realiza- dos es de unos 20ms para una resolución de 4096 muestras.
Para paliar con el error humano se ha desarrollado el concepto de retraso corrector. Aunque el uso del mismo atentaría a la condición temporal impuesta, con él se consigue eliminar toda perturbación de la señal de entrada, de modo que dependiendo del uso que se le esté dando al plugin, puede ser o no beneficioso. Por ejemplo, para loops en los que no se necesita escuchar la conversión en tiempo real, sino cuando se repite el loop, es muy útil esta herramienta combinada con una compensación de pista adecuada.
Referencias
[2] http://www.ts-audiotomidi.programas-gratis.net
[4] http://www.css-audiovisual.com/areas/guias/midi.htm
[5] Menzies-Gow D., An investigation into the design of musical performance instruments. Music Technology MSc, University of York, 1995.
[6] Rocchesso D., Introduction to Sound Processing, Università di Verona, Dipartimento di Informatica.
[7] Zölzer U., DAFX: Digital Audio Effects, Second Edi- tion. Helmut Schmidt University, Hamburg, Germany, John Wiley & Sons, 2011. Ltd. ISBN: 978-0-470- 66599-2.