En estos momentos de precio de la electricidad tan altos, uno de los temas que suscitan más extrañeza en el público es el modelo marginalista.
Por su interés, hemos rescatado el documento escrito en 2012 por José Luis Sancha “Fundamentos teóricos del modelo marginalista”, que apareció anexado a su artículo publicado en la revista ANALES “El Sistema Eléctrico Español (VII). Mercado eléctrico. 2ª Parte”. Este artículo formaba parte de una serie de diez artículos del autor en torno al Sistema Eléctrico Español, germen de su posterior libro “Presume de entender (a fondo) las facturas de la luz y del gas” 2016. Ed. Comillas.
José Luis Sancha ha escrito la siguiente nota introductoria.
En su aparente simplicidad, el modelo marginalista se asienta en potentes fundamentos económicos y, al mismo tiempo, contiene importantes condicionantes, tanto estructurales como coyunturales, que podrían limitar su aplicabilidad.
Confío en que la difusión de este escrito contribuya positivamente al debate abierto actualmente en la sociedad para encontrar la solución más eficiente y justa a los altos precios de la electricidad, agudizados por la guerra desatada por Rusia en Ucrania, que permita la recuperación de las inversiones, sin beneficios extraordinarios, y que transmita las señales adecuadas para asegurar la satisfacción de la demanda en todo momento.
Introducción
Los fundamentos marginalistas en el mercado eléctrico se asientan en un principio general y tres grandes cuestiones a resolver.
El principio general es que un sistema descentralizado y de competencia perfecta, conduce a los mismos resultados a los que llegaría un sistema centralizado con información completa de todos los parámetros del sistema eléctrico [1]. Como ya fue mencionado en el artículo anterior, este principio quedaba explícitamente reflejado en la Ley 54/1997 del Sector Eléctrico, en cuya exposición de motivos se decía: “La gestión económica del sistema abandona las posibilidades de una optimización teórica para basarse en las decisiones de los agentes económicos en el marco de un mercado mayorista organizado de energía eléctrica.”
Primera cuestión. Operación
La primera gran cuestión que se plantea es el problema de la operación en un momento dado: ¿qué generadores deben operar y cuánta energía debe producir cada uno y a qué precio?, así como su correlativa: ¿qué demanda debe ser satisfecha, en qué forma y a qué precio?
En un sistema centralizado que dispusiese de toda la información, tanto de los costes de la generación como de las preferencias de la demanda valoradas económicamente, las decisiones anteriores estarían guiadas por el principio de maximizar el beneficio social: diferencia entre la utilidad de la demanda y los costes de la generación [2].
El punto de equilibrio entre la potencia generada y la demandada que maximiza el beneficio social se da cuando el coste marginal de la generación €/MWh se iguala con la utilidad marginal de la demanda €/MWh.
En el caso simplificado en el que sólo se consideraran los costes variables de operación [3] en el lado de la generación, esto se traduciría, en asegurar en primer lugar el funcionamiento del generador con menores costes marginales (en este caso, menores costes variables) hasta su potencia límite, luego del generador con los siguientes menores costes marginales hasta su potencia límite, etc. En el lado de la demanda, quedaría satisfecha la demanda de mayor utilidad marginal (la que más valora recibir energía eléctrica €/MWh), luego la siguiente demanda de mayor utilidad marginal, y así sucesivamente.
Esto se traduciría, en el lado de la generación, en asegurar en primer lugar el funcionamiento del generador con menores costes marginales hasta su potencia límite, luego del generador con los siguientes menores costes marginales hasta su potencia límite, etc. En el lado de la demanda, quedaría satisfecha la demanda de mayor utilidad marginal (la que más valora recibir energía eléctrica €/MWh), luego la siguiente demanda de mayor utilidad marginal, y así sucesivamente.
En el punto de corte, el coste marginal del último generador conectado es igual a la utilidad marginal de la última demanda satisfecha. Intuitivamente puede verse que el óptimo se alcanza cuando 1 MWh adicional de energía producida supondría para el sistema un coste mayor que la utilidad obtenida por ese MWh adicional de demanda. Dicho de otra forma, el óptimo se alcanza cuando 1 MWh menos de energía producida supondría para el sistema un ahorro de coste inferior a la utilidad perdida por ese MWh menos de demanda.
De forma simplificada, pueden considerarse dos grandes bloques en los costes de un generador: costes fijos (costes relativos a la inversión, personal, etc.), en los que se incurre, aunque el generador no esté produciendo energía, y costes variables dependiendo de la potencia generada (fundamentalmente costes relativos al combustible utilizado). Es importante resaltar que el coste de producir un MWh adicional (coste marginal) de cada generador es absolutamente independiente de sus costes fijos. Intuitivamente, de nuevo, los costes fijos ya están asumidos, así que generar 1 MWh adicional tiene un coste que no depende del bloque de costes fijos sino del bloque de los costes variables.
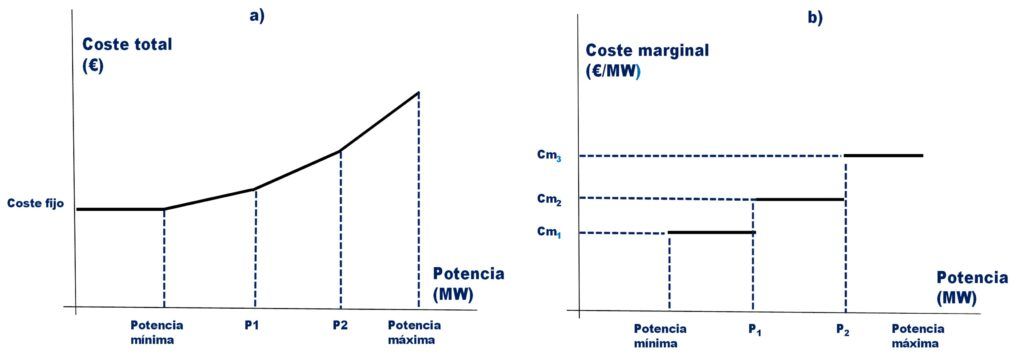
En la fig. 1.a) puede verse un ejemplo del coste de un generador dependiendo de la potencia de funcionamiento del mismo. En la fig. 1.b) aparece el coste marginal de dicho generador, que en este caso presenta tres valores (cm1, cm2 y cm3) según el rango de potencia utilizado.
FIGURA 1
Coste total a) y coste marginal b) de un generador
en función de su potencia de funcionamiento
En un sistema descentralizado, los generadores y las demandas acuden al mercado con sus ofertas de venta y compra respectivamente. En este caso, las decisiones de los agentes estarían guiadas, no por el principio de maximizar el beneficio social, sino por el de maximizar su propio beneficio.
Pues bien, es fácil demostrar que el precio de oferta óptimo del generador (en ausencia de poder de mercado) es su coste marginal, y que el precio de oferta óptimo de la demanda es su utilidad marginal. En efecto, tal como se ve en la fig. 1, la escalera de precios de la oferta se construye con los costes marginales de los generadores mientras que la escalera de precios de la demanda se construye con la utilidad variable de los puntos de demanda. De nuevo, el punto de corte de ambas escaleras indica la cantidad de energía producida-demandada y el precio óptimo de intercambio, donde se igualan el coste marginal del último generador necesario y la utilidad marginal de la última demanda satisfecha.
Todos los generadores con menores costes marginales que el precio de corte (los situados a la izquierda de la energía de corte) reciben el precio de corte, de la misma forma que todas las demandas con mayores utilidades pagan el precio de corte. Los generadores con mayores costes y las demandas con menores utilidades (situados a la derecha de la energía de corte) ni producen ni reciben energía.
Cualquier otra solución no sería óptima para el conjunto y desde luego no sería viable a la larga. En efecto, si cualquier pareja generador-demanda situados a la izquierda de la energía de corte intercambiasen energía a un precio inferior al de corte, se estaría produciendo una transferencia de renta del generador a la demanda y no sería una solución de equilibrio ya que el generador actuaría para obtener un precio mejor con demandas dispuestas a pagarlo.
De forma similar, si cualquier pareja generador-demanda situados a la izquierda de la energía de corte intercambiasen energía a un precio superior al de corte, se estaría produciendo una transferencia de renta desde la demanda al generador y no sería una solución de equilibrio ya que la demanda actuaría para obtener un precio mejor con generadores dispuestos a producirlo.
Segunda cuestión. Nuevas inversiones
La segunda gran cuestión que se plantea es el problema de la inversión: ¿qué nuevos generadores deben incorporarse al sistema?
En un sistema centralizado que dispusiese de toda la información, las decisiones de inversión en generación estarían guiadas por el principio de maximizar la diferencia entre el beneficio social obtenido por las decisiones de operación antes vistas (utilidades de la demanda menos costes de la generación) y los costes de las inversiones a largo plazo [4].
El óptimo se obtiene cuando el incremento marginal de beneficio social en la operación se iguala con la inversión marginal a largo plazo en generación. Intuitivamente puede verse que es el óptimo: 1 MWh adicional de energía introducida en el sistema supondría un coste de inversión mayor que el aumento de beneficio social proporcionado en la operación a corto de ese MWh.
En un sistema descentralizado, las decisiones de inversión de los generadores están guiadas por el principio de maximizar su propio beneficio. En términos matemáticos, se trata del mismo tipo de problema que en el caso centralizado y, de nuevo, la solución óptima es la misma que en ese caso. Para el generador, el punto de equilibrio indica que 1 MWh adicional de energía introducida en el sistema supondría un coste de inversión mayor que el aumento del beneficio que le proporcionaría la operación a corto de ese MWh.
En aquellos casos en que, bien por la existencia de cuotas o cupos, bien por concesiones administrativas, o por cualquier otra razón, esté limitado el libre acceso a la instalación de determinadas tecnologías de generación [5] , lo relevante sería que se aplicasen mecanismos de mercado para determinar los proyectos de inversión seleccionados.
Tercera cuestión. Recuperación de inversiones
La tercera gran cuestión que se plantea es el problema de la recuperación de inversiones: ¿son suficientes los precios obtenidos por los generadores para que éstos recuperen sus inversiones en el largo plazo?, o dicho de otra forma ¿cómo recuperan los generadores los costes fijos de producción si el precio se forma únicamente en base a los costes marginales de producción?
La respuesta a esta pregunta es la misma tanto para un sistema centralizado como para uno descentralizado. La explicación conceptual [6] es que, en los generadores de costes marginales inferiores al precio, la diferencia entre el precio y su coste variable es lo que permite recuperar su coste fijo.
Aunque el problema es el mismo para todas las unidades, es habitual la preocupación de los generadores que únicamente funcionan en los momentos de punta del sistema. En efecto, si el precio queda fijado por los costes marginales de esos generadores ¿cómo pueden recuperar sus costes fijos?
La respuesta teórica es clara: gracias a las rentas percibidas durante los periodos de escasez. En efecto, cuando la demanda excede a la generación, el punto de corte se produciría para un precio igual a la utilidad de la demanda, que en general será mayor que los costes marginales de la central de punta. Esto llevaría, probablemente, a que en ciertas horas al año el precio de la energía podría alcanzar valores muy altos [7], lo cual, por otro lado, actuaría como incentivo para la instalación de generación de punta. Desde un punto de vista teórico, la solución a esta dificultad sería que en esos momentos de punta fuese la demanda la que fijase los precios valorando adecuadamente la energía no suministrada, con lo que el precio recibido por los generadores (por todos los generadores, no solo los de punta) compensaría la totalidad de sus costes.
Si se consideran inaceptables (por la demanda o por el regulador) las horas de escasez, una posible solución alternativa consiste en que el sistema compense, fuera de mercado, a la generación mediante determinados incentivos para asegurar su contribución en los momentos de punta [8]. De esta forma, se buscaría garantizar la cobertura de toda la demanda y contener los precios de punta, aunque la dificultad de esta solución fuera de mercado es encontrar el incentivo “adecuado” que asegure el objetivo al mínimo coste.
Referencias
[1] Un desarrollo completo puede verse en “Principios económicos marginalistas en los sistemas de energía eléctrica”, José Ignacio Pérez-Arriaga, 1994.
[2] En términos matemáticos, se trata de un problema de optimización sujeta a restricciones (los límites operativos de los generadores). La solución matemática más elegante se obtiene mediante la función de Lagrange del objetivo a maximizar.
[3] Sin considerar los costes de arranque, de acoplamiento, etc.
[4] En términos matemáticos, se trata de un problema similar al anterior.
[5] Se da, por ejemplo, en algunas modalidades que utilizan energías renovables: solar, eólica e hidráulica.
[6] La demostración completa puede encontrarse en Pablo Rodilla Rodríguez. Tesis Doctoral. IIT 2010.
[7] Algunos estudios estiman que la utilidad marginal de la demanda en momentos de punta podría ser 10 o incluso 100 veces superior a la normal.
[8] Esta es la que se aplica en España. Los consumidores costean estos incentivos a través del pago por capacidad de la factura eléctrica.
